ANN의 발전과 구조

앨런 튜링 - Can machines think?

앨런 튜링의 논문, <Computer Machinery and Intelligence>의 일부

인간은 오랜 세월 동안 기계가 인간처럼 사고할 수 있을지 호기심을 가져왔습니다. 1950년, 엘런 튜링(Alan Turing)은 자신의 논문 <Computer Machinery and Intelligence>에서 “Can machines think?”라는 질문을 던지며, 기계의 지능에 대한 논의를 본격적으로 시작했습니다.

그는 이 질문에 답하기 위해 인간과 기계의 대화를 통해 기계의 지능을 평가하는 튜링 테스트를 제안했는데, 이러한 호기심과 도전은 인간의 지능을 모방하고 이를 넘어서는 시스템을 설계하기 위한 다양한 시도로 이어졌습니다.

특히 인공신경망(Artificial Neural Network, ANN)은 생물학적 뉴런의 작동 방식을 본뜬 알고리즘으로, 기계가 데이터를 학습하고 패턴을 인식하는 방식을 혁신적으로 변화시켰습니다. ANN의 발전은 초기의 단순한 뉴런 모델에서 시작해 오늘날의 딥러닝으로 이어지며, 기계 지능의 가능성을 증명하는 데 큰 역할을 해왔습니다. 오늘은 이러한 신경망의 역사를 통해 인공신경망이 어떻게 발전해 왔는지 살펴보고자 합니다.

인간의 뉴런을 기계적으로 구현한 첫 모델, M-P 뉴런

인간의 지능을 모방하기 위한 시도는, 인간의 생물학적인 뉴런을 모방한 논리적 모델로부터 시작했습니다. 1943년, 워렌 맥컬록(Warren McCulloch)과 월터 피츠(Walter Pitts)는 <A Logical Calculus of Ideas Immanent in Nervous Activity>라는 논문을 발표하고, 뉴런의 동작을 이진 논리로 설명하는 M-P 뉴런을 소개했습니다.

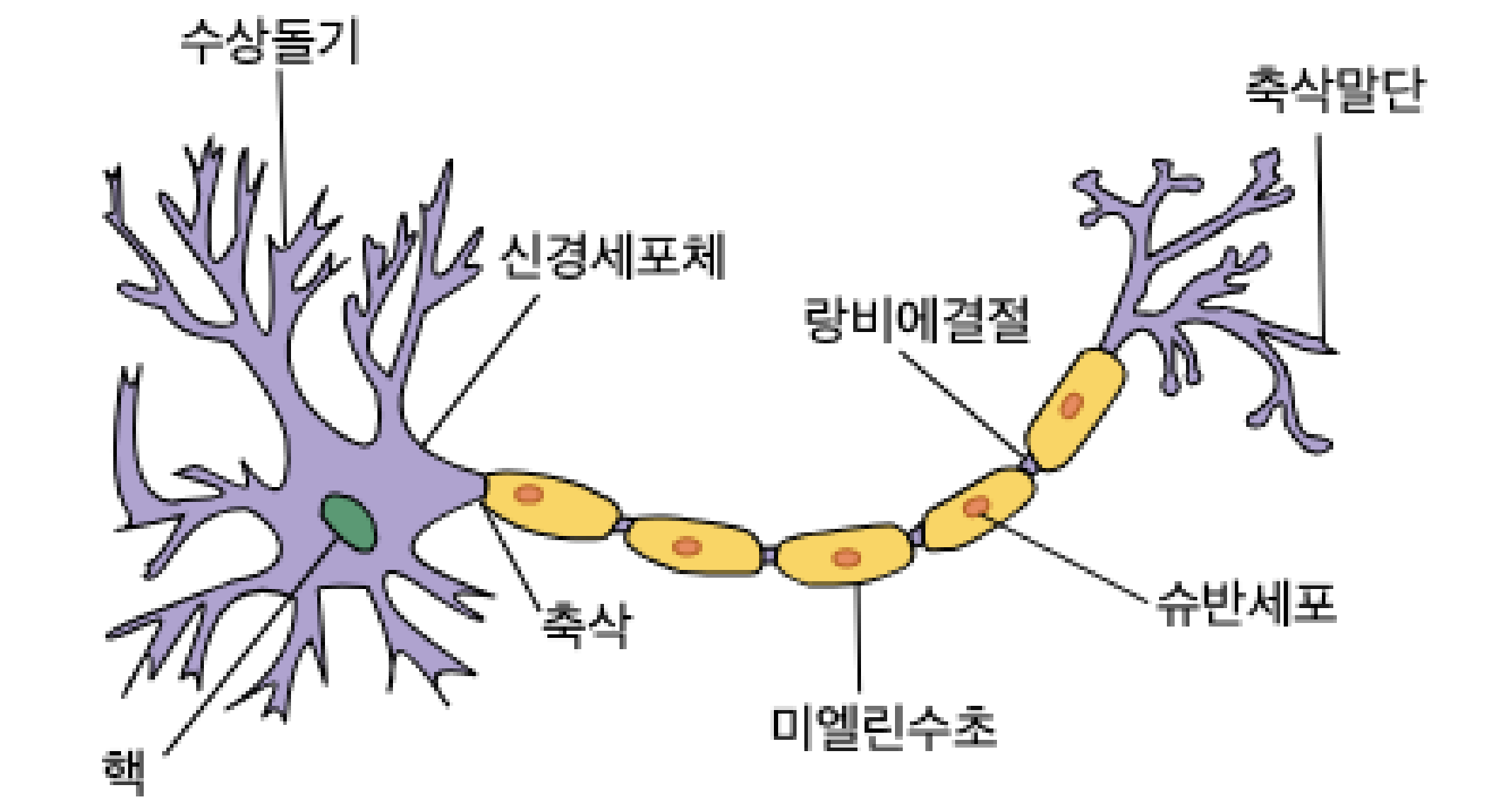
생물학적 뉴런의 구조

생물학적 뉴런의 구조 (출처)

인간의 뇌는 수백억 개의 뉴런으로 이루어져 있고, 각 뉴런은 신호를 처리한 뒤 다른 뉴런으로 신호를 전달합니다. 뉴런의 수상돌기에서 신호를 받아들이면, 신경세포체에서 받은 신호를 종합하고 처리하죠. 계산 결과가 특정 임곗값을 초과하면 축삭 말단 부근의 시냅스를 통해 다음 뉴런으로 신호가 전달되며, 뇌 전체에서 이 과정을 반복해 정보를 처리합니다.

M-P 뉴런

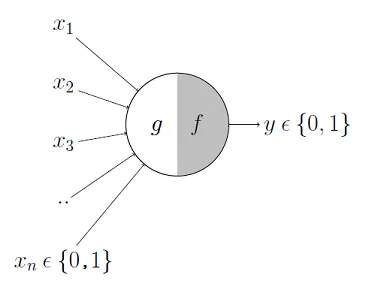
M-P 뉴런 (출처)

앞서 살펴본 생물학적인 뉴런의 동작을 단순화한 수학적 모델인 M-P 뉴런은 위와 같이 그릴 수 있습니다. 인간의 뉴런이 수상돌기에서 여러 입력 신호를 받는 것처럼, M-P 뉴런에도 2진 값을 가진 여러 개의 입력값($x_1$, $x_2$, …, $x_m$)이 전달됩니다. 그런 다음, 신경세포체에서 신호를 종합하고 다음 뉴런으로의 신호 전달 여부를 결정할 때 임계값이 필요했듯이, M-P 뉴런에서도 입력값의 합이 특정 임계값을 초과하면 뉴런이 활성화되어 1이, 그렇지 않으면 뉴런이 비활성화 되어 0이 출력됩니다. 임계값을 조정함으로써 기본적인 논리 회로(AND, OR, NOT)를 구현할 수 있고, 여러 개의 뉴런을 계층적으로 결합함으로써 조금 더 복잡한 계산도 가능해집니다.

이어 1949년, 캐나다의 심리학자 도널드 올딩 헵(Donald Olding Hebb)은 ‘헵의 이론(Hebbian theory)’을 발표하며 동시에 활성화되는 뉴런들은 함께 연결되고 함께 강화한다고 제안했습니다. 활동 중 함께 발화(활성화)하는 뉴런들은 강해진다는 생물학적 법칙에서 출발한 헵의 이론은 이후에 가중치를 활용한 신경망 학습 알고리즘의 기반이 됩니다.

인공지능의 본격적인 등장, 퍼셉트론

인공지능의 선구자로 불리는 미국의 전산학자 존 매카시(John McCarthy)는 1956년, 다트머스 대학 학회(Dartmouth Conference)를 개최하고 ‘인공지능’이라는 용어를 처음으로 사용했습니다. 인공지능(Artificial Intelligence, AI)을 ‘기계를 인간 행동의 지식에서와 같이 행동하게 만드는 것’으로 정의했는데, 이때를 시작으로 관련 연구들은 ‘인공지능’이라는 이름을 내걸고 더욱 활발해졌습니다. 머지않아 1958년, 최초의 인공 신경망인 퍼셉트론(Perceptron)이 등장합니다.

퍼셉트론

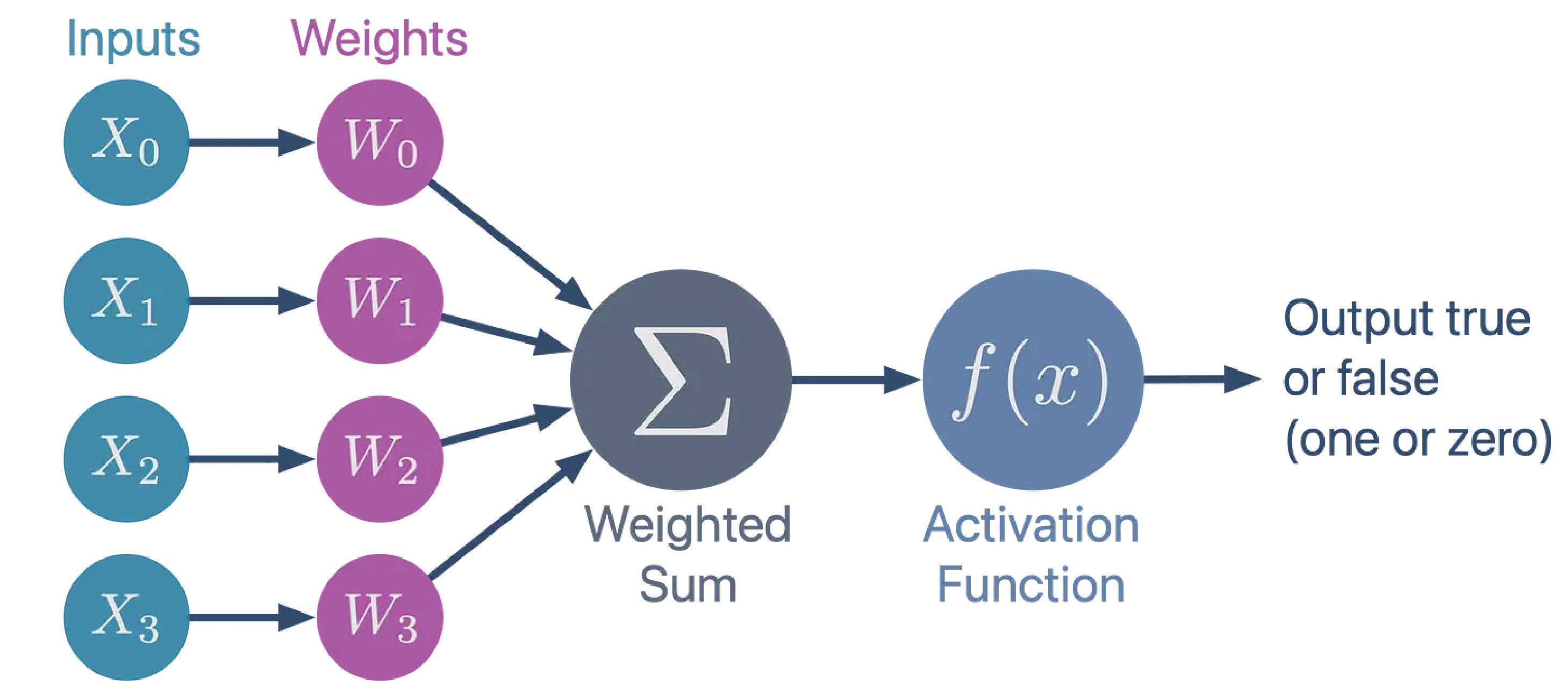
퍼셉트론 (출처)

미국의 심리학자 프랑크 로젠블랫(Frank Rosenblatt)은 맥컬록-피츠의 모델과 헵의 이론에서 영감을 얻어 가중치와 학습의 개념을 추가한 퍼셉트론을 개발했습니다. 입력값마다 각각 입력의 중요도를 나타내는 가중치를 곱한 후 모두 합해 활성화 함수에 전달합니다. 활성화 함수에서 출력되는 결과를 보고 앞서 곱해진 가중치(weights)를 조정해 출력된 예측값과 정답의 오차를 줄이는 학습 알고리즘이 포함된 것이죠.

계단 함수

계단 함수 (출처)

초기 퍼셉트론에서 사용된 활성화 함수는 위 그래프처럼 임곗값(threshold)을 기준으로 출력이 0 혹은 1로 바뀌는 계단 함수(step function)였습니다. 활성화 함수는 이처럼 가중치가 반영된 입력값의 총합이 뉴런의 활성화를 일으키는지를 결정하는 역할을 합니다. 현대에 들어서는 더 다양한 활성화 함수들이 있는데, 이 부분은 뒤에서 인공신경망의 학습을 다루면서 더 살펴보겠습니다.

퍼셉트론이 해결하지 못한 문제, XOR

퍼셉트론이 등장하면서 인공지능에 대한 연구는 부흥기를 맞이했지만, 그 기간은 그리 길게 이어지지 못했습니다. 1969년, 미국의 컴퓨터 과학자 마빈 리 민스키(Marvin Lee Minsky)가 저서 <Perceptrons>에서 퍼셉트론은 XOR 문제와 같은 비선형 문제를 해결할 수 없다는 한계를 지적했기 때문입니다.

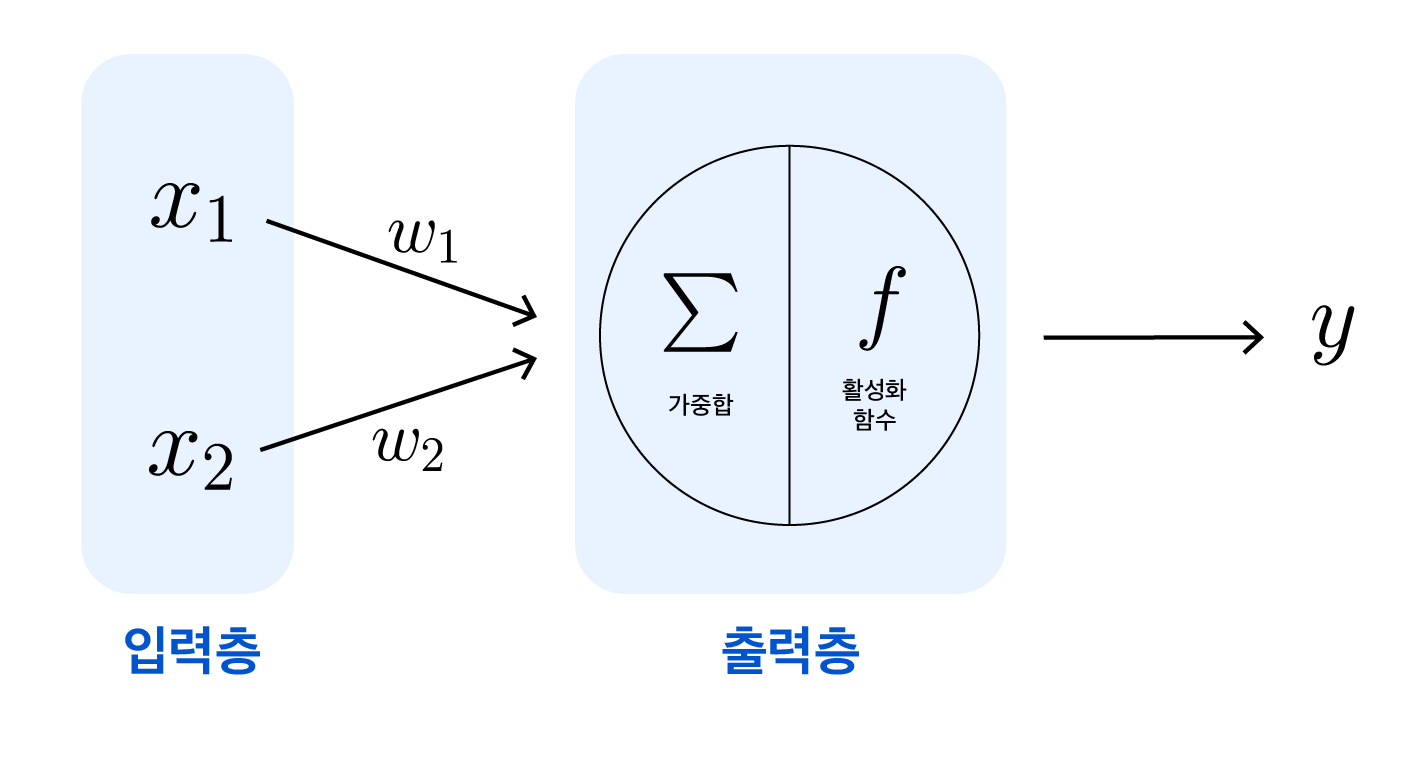
퍼셉트론의 층

초기의 퍼셉트론은 값을 입력받는 입력층과, 출력값을 결정하는 출력층까지 총 두 단계로만 이루어진 단층 퍼셉트론이었습니다. 이러한 단층 구조는 입력값을 선형 결합해서 단일한 출력만을 낼 수 있기 때문에, 비선형 경계를 표현하는 데에 한계가 있습니다.

대표적인 비선형 문제 중 하나인 XOR 회로를 그림으로 나타내면 아래와 같습니다.

논리회로

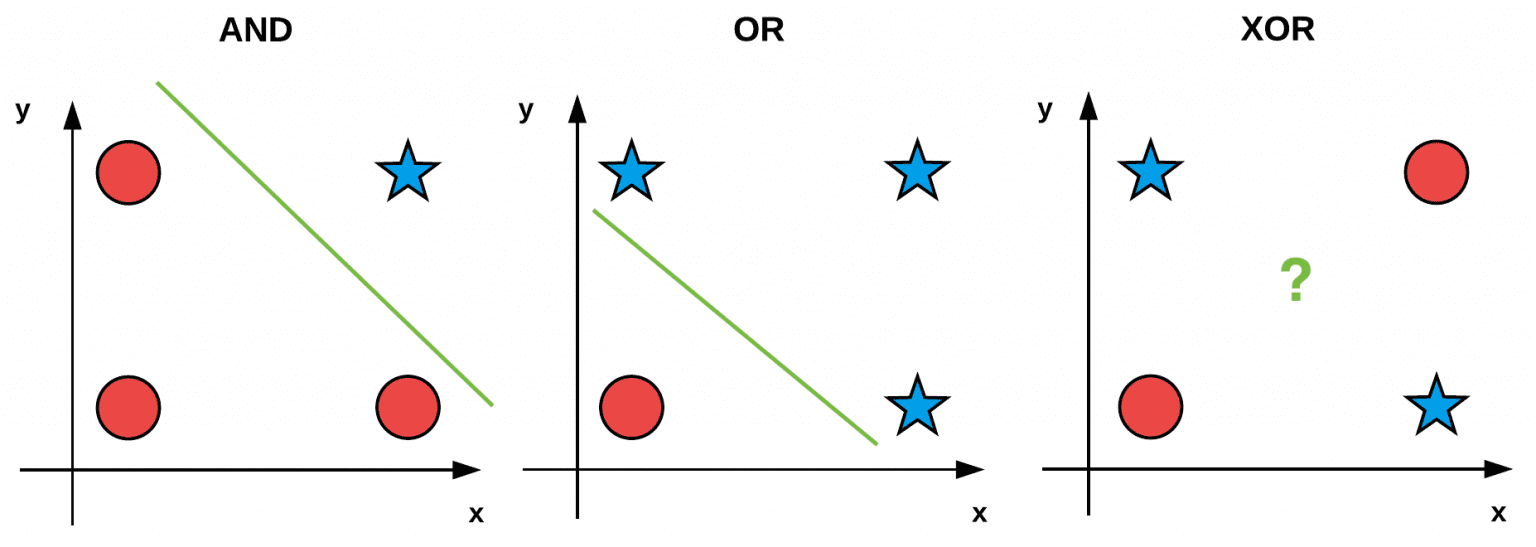
논리 회로 (출처)

다른 논리 회로인 AND 회로와 OR 회로는 선형적인 경계로 데이터를 분리할 수 있지만, XOR 회로에서는 데이터를 표현할 하나의 선형 경계를 그릴 수 없습니다. 단층 구조라서 선형 경계만을 그릴 수 있는 퍼셉트론의 한계가 여기서 나타난 것이죠. 이후 인공 신경망 연구에는 오랜 침체기가 찾아왔습니다.

다층 신경망과 역전파 알고리즘

퍼셉트론이 단층 신경망이라서 위와 같은 문제를 갖는 것이라면, 여러 층을 갖는 퍼셉트론은 이 문제를 해결할 수 있을까요?

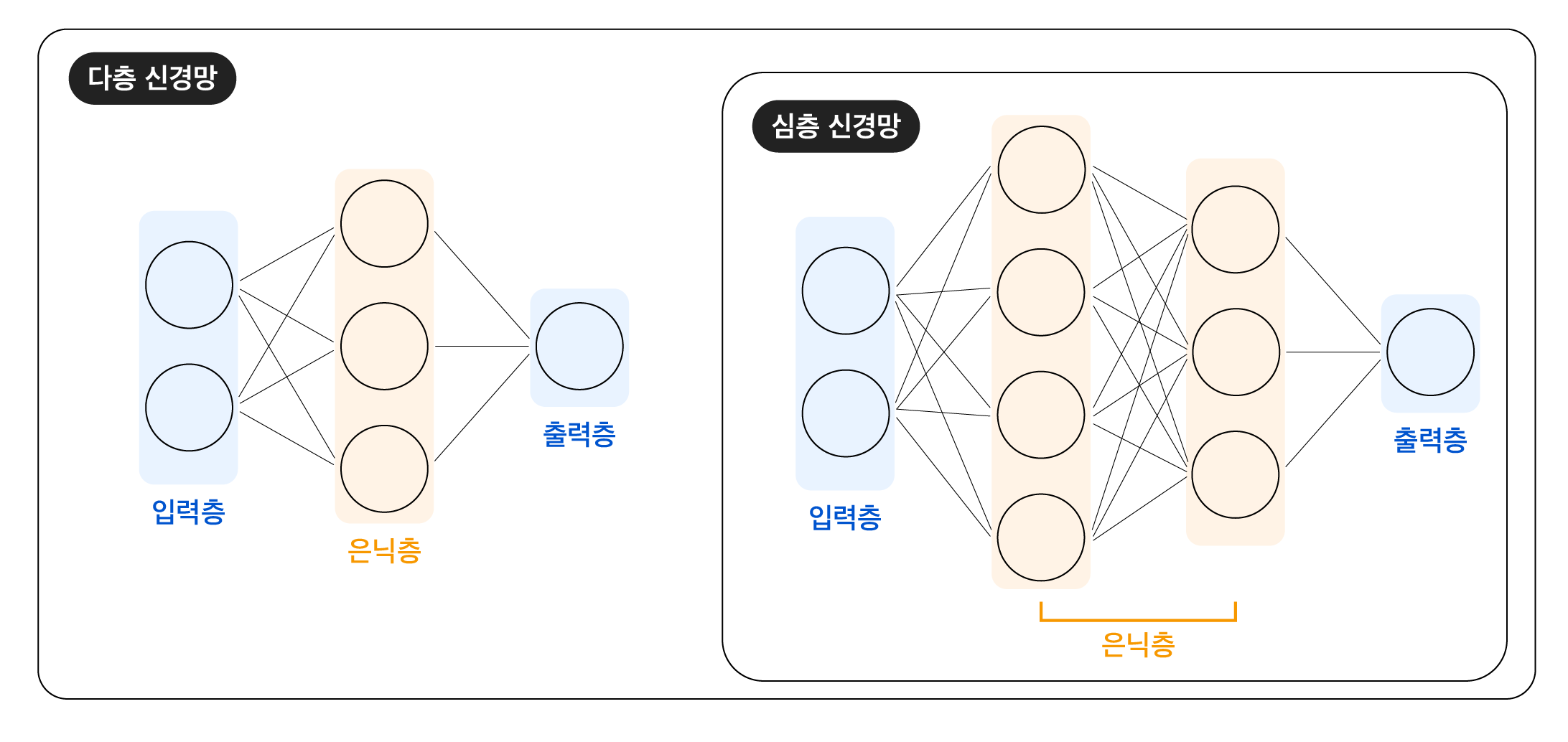
다층신경망

다층 신경망은 단층 신경망에 하나 이상의 은닉층이 추가된 인공 신경망입니다. 은닉층이 2개 이상이면 심층 신경망(Deep Neural Network, DNN)이라고도 합니다. 각 층은 그림에서 동그라미로 표현된 노드로 구성되어 있습니다. 여기서 노드(node)는 앞서 계속 다뤄온 인공 뉴런을 의미합니다. 앞으로 인공 신경망을 구성하고 있는 인공 뉴런을 노드라고 표기하겠습니다. 입력층의 노드에는 입력 데이터가 들어있지만, 나머지 층의 노드는 각자 정해진 역할을 수행합니다. 그 역할의 내용은 다음과 같습니다.

입력층 (Input Layer): 입력 데이터의 전달
은닉층 (Hidden Layers):
- 입력층에서 입력 데이터를 전달받거나 직전 은닉층의 계산 결과를 전달받음
- 전달받은 값에 각각 가중치를 곱해 합산하고, 활성화 함수를 통해 다음 노드에 전달할 값 결정
출력층 (Output Layer): 신경망의 최종 출력 계산

오랜 시간 동안 많은 연구자들이 노력했지만, 다층 신경망을 구현하는 것은 어려웠습니다. 은닉층에서 도출되는 각 노드의 출력값에는 오차를 측정할 정답이 없어, 은닉층의 가중치를 조정할 기준이 없었기 때문입니다. 그러나 1986년, 영국의 컴퓨터 과학자 제프리 힌튼(Geoffrey Hinton)이 다른 연구자들과 함께 다층 신경망을 학습시킬 수 있는 오류 역전파 알고리즘을 고안해 냈습니다.

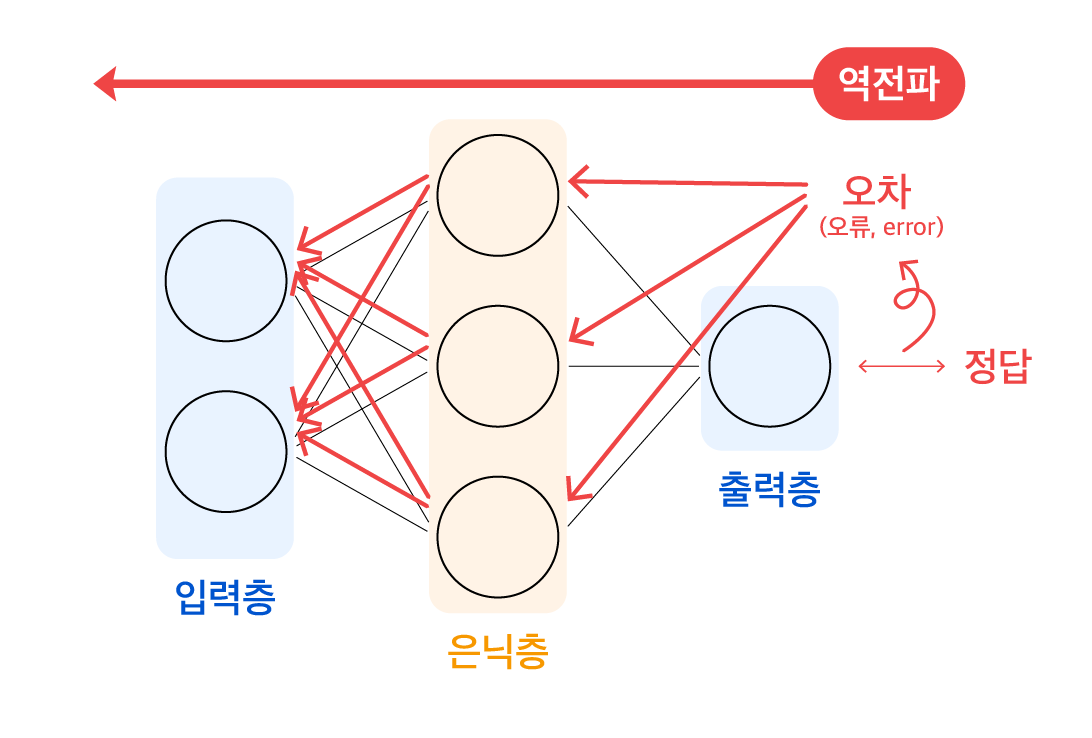
오류 역전파 알고리즘

정답이 있는 출력층에서 오차를 계산해 낼 수 있고, 이 오차(오류)를 출력층에서 입력층 방향으로 역으로 전파시키면서 은닉층의 가중치들을 재조정할 수 있게 된 것입니다. (역전파 알고리즘에 대해서는 이후 ANN의 학습에서 더 자세히 알아보겠습니다.) 오류 역전파 알고리즘으로 다층 신경망을 구현해 내면서, 이후에는 순환 신경망(RNN)과 합성곱 신경망(CNN)과 같은 구조들이 등장하여 시계열 데이터와 이미지 데이터를 처리할 수 있게 되었습니다.

현대의 인공 신경망, 은닉층에서의 동작

다층 신경망은 현대 인공 신경망의 기본 구조로 자리 잡았습니다. 이 현대 인공 신경망의 중요한 구성 요소 중 하나인 은닉층에 대해 조금 더 자세히 알아보겠습니다. 은닉층의 각 노드에서는 다음의 과정들이 순서대로 진행됩니다.

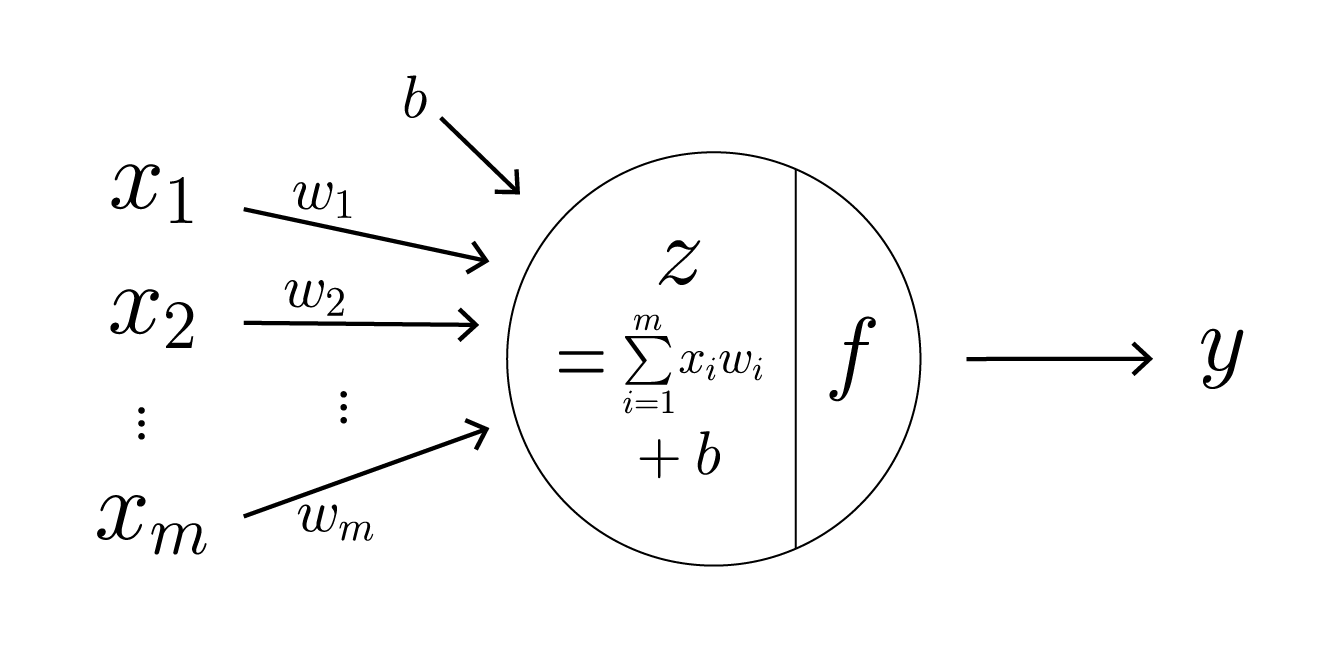
은닉층 동작

입력 데이터와 가중치(Weights)의 곱 계산
계산한 곱과 편향(Bias)을 더함
활성화 함수(Activation Function) 적용 결과 출력

하나씩 살펴보겠습니다.

1) 입력 데이터와 가중치(Weights)의 곱 계산

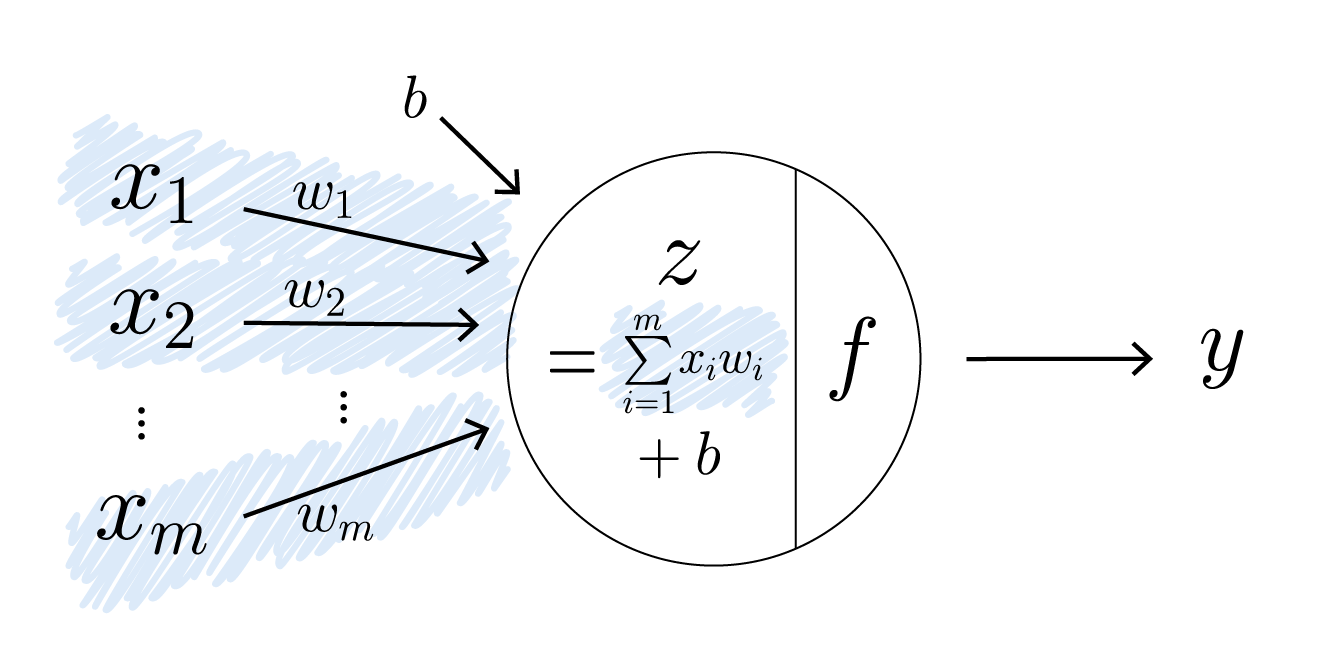
은닉층 동작 1

노드로 입력 데이터들이 전달되면, 각 입력값에 맞는 가중치가 곱해집니다. 가중치는 각 입력값에 대한 중요도를 나타내는 숫자입니다. 따라서 입력값에 가중치를 곱함으로써 중요한 값은 비중을 키우고, 그렇지 않은 값은 비중을 줄일 수 있습니다.

2) 계산한 곱과 편향(Bias)을 더함

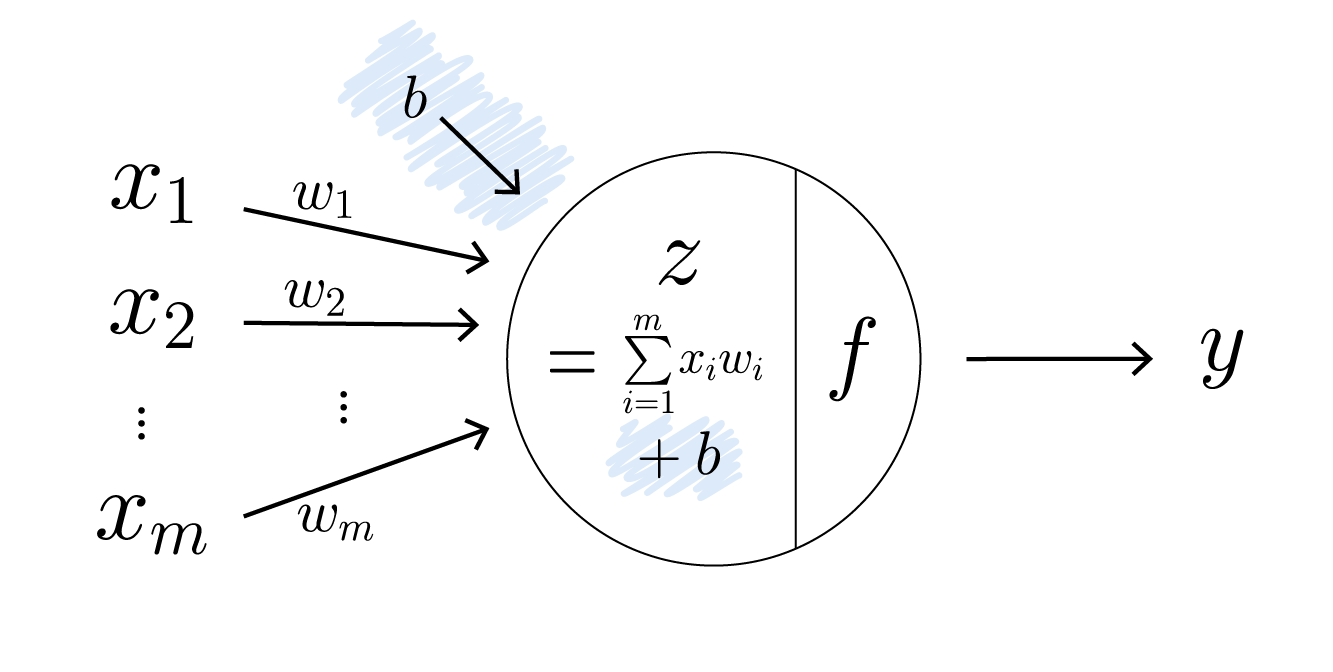
은닉층 동작 2

앞서 계산한 곱에 편향을 더해, 활성화 함수에 전달할 값을 결정하는 선형 변환 식 ($z=w_1x_1+w_2x_2+…+w_mx_m+b$)을 완성합니다. 입력값과 가중치의 곱에 편향을 더함으로써, 입력값이 0일 때도 유의미한 출력을 만들어낼 수 있도록 값을 조정합니다.

3) 활성화 함수(Activation Function) 적용 결과 출력

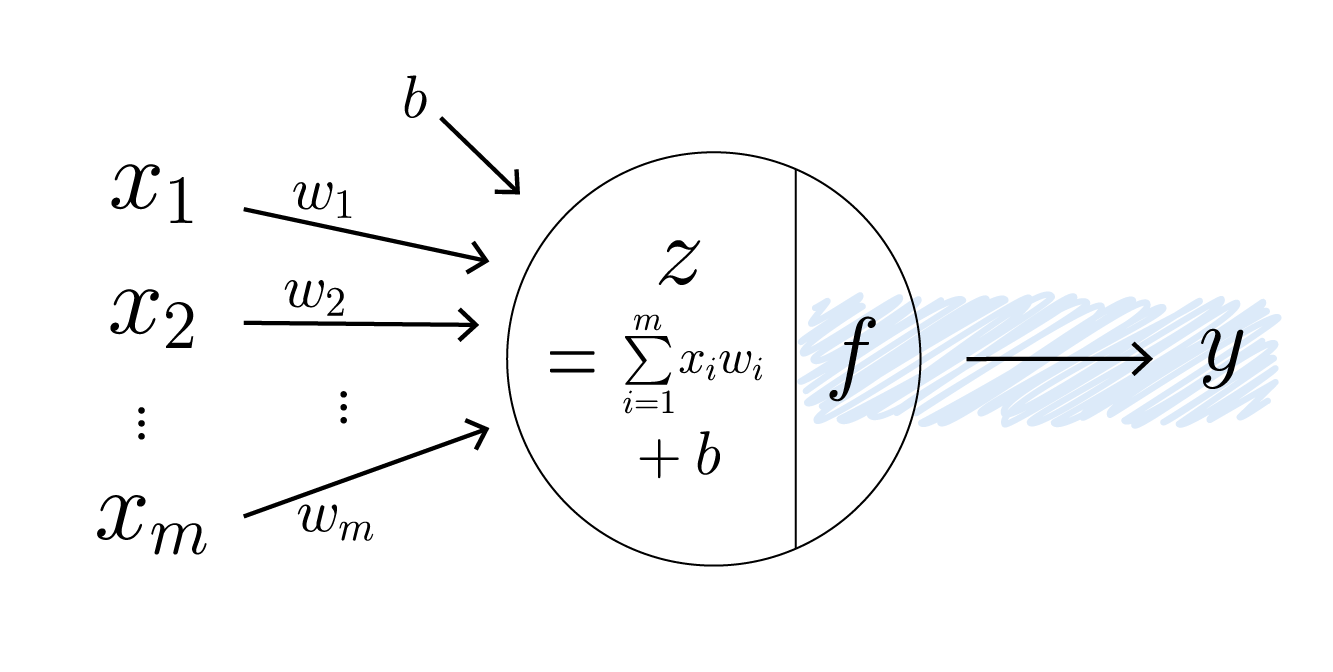
은닉층 동작 3

선형 변환된 값을 해당 노드의 출력값으로 변환하기 위해 활성화 함수를 사용합니다. 활성화 함수를 사용하는 주된 목적은 출력값에 비선형성을 추가하기 위함입니다. 선형 변환만을 사용한 신경망은 직선으로 데이터를 표현할 수 있는 경우에만 한정되어 있습니다. 선형 변환을 아무리 많이 결합해 봤자, 여러 층의 선형 변환은 결국 하나의 선형 모델과 동일한 결과를 내기 때문입니다. 하지만 복잡한 문제는 직선이 아닌, 보다 복잡한 모양의 경계(곡선, 면 등)가 필요한 경우가 많습니다. 활성화 함수는 이러한 비선형 경계를 만들 수 있도록 신경망에 비선형성을 도입합니다.

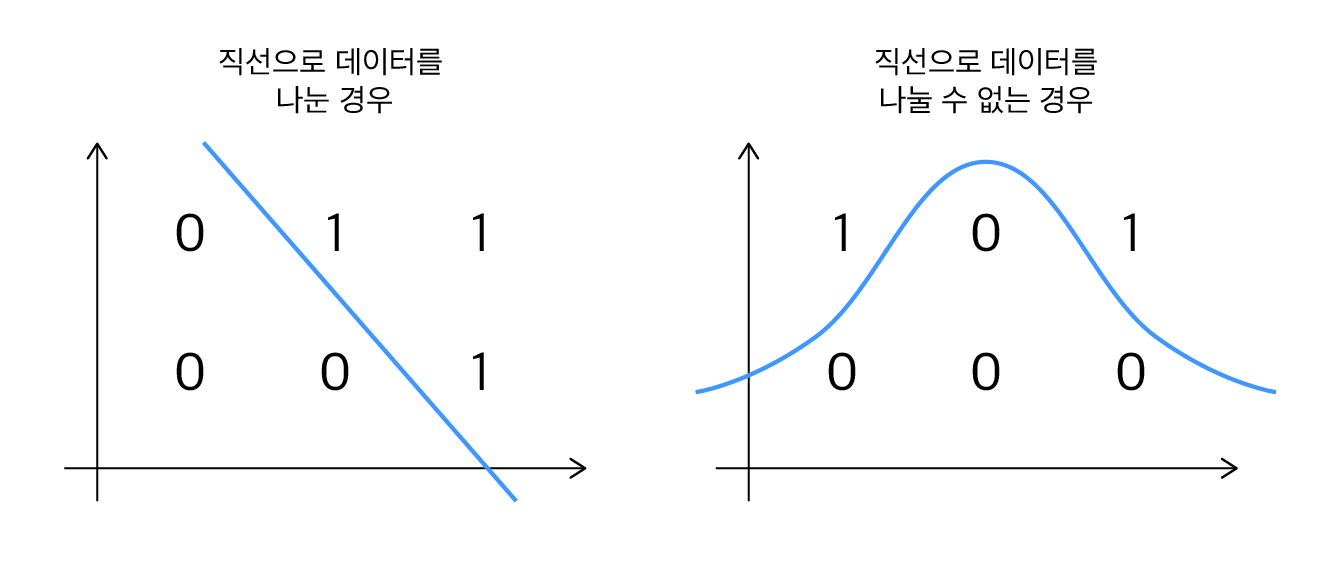
활성화 함수의 비선형성

대표적인 활성화 함수로는 시그모이드 함수가 있습니다.

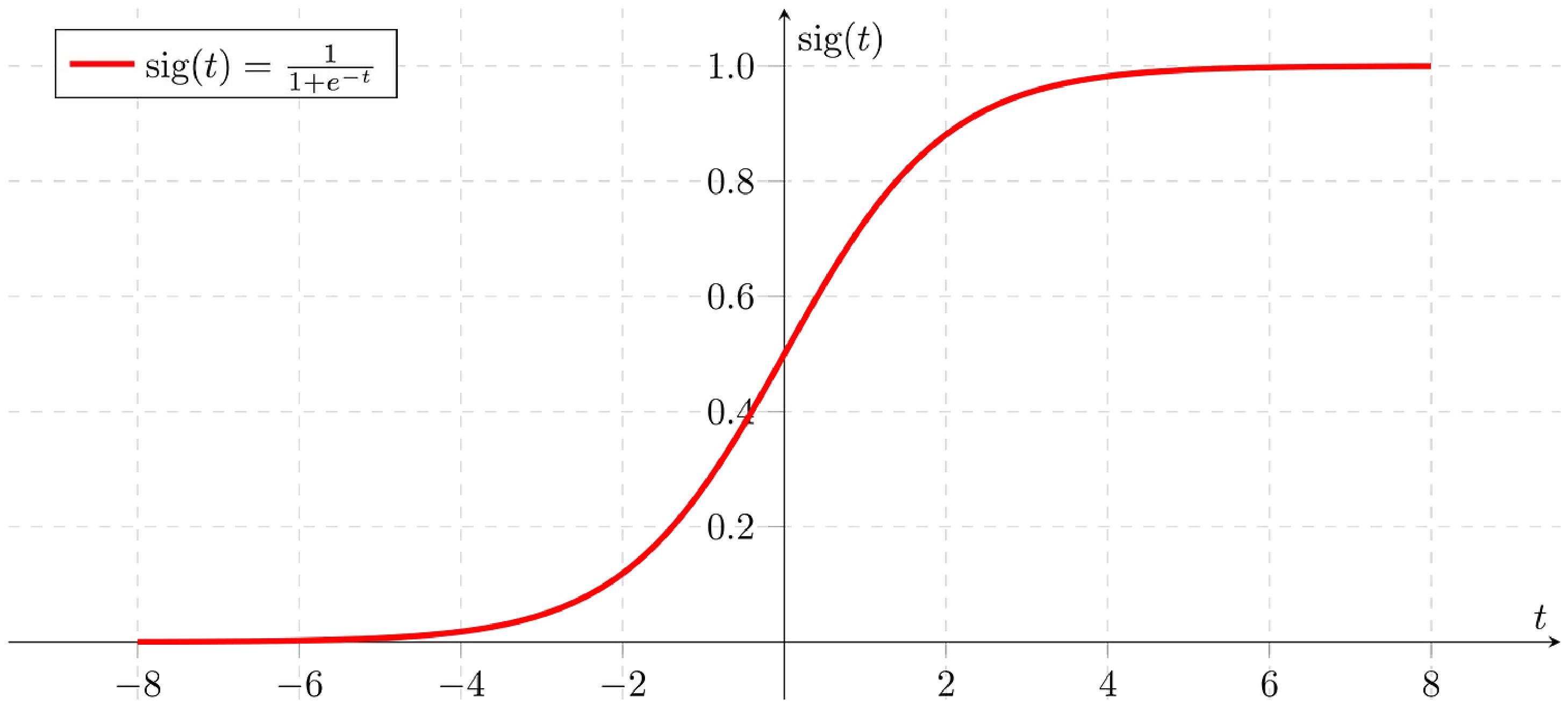
시그모이드 함수

시그모이드 함수 (출처)

시그모이드 함수는 실수 전체의 입력값에 대해 출력값이 0과 1 사이로 한정되어 있기 때문에, 특정 입력이 참인지 거짓인지를 분류하는 이진 분류(Binary Classification) 문제에서 사용됩니다. 시그모이드 함수의 출력값이 참 혹은 거짓 중 하나의 클래스에 속할 확률로 이해할 수 있기 때문입니다.

마무리

인공신경망(ANN)의 발전 과정은 인간의 지능을 모방하려는 도전에서 시작해, 학습 가능성과 문제 해결 능력을 점차 확장해 온 여정이었습니다. M-P 뉴런과 퍼셉트론은 초기의 중요한 기반을 마련했지만, XOR 문제와 같은 비선형 문제를 해결하지 못하며 한계를 드러냈습니다. 이러한 한계를 극복하기 위해 다층 신경망과 오류 역전파 알고리즘이 도입되었고, 이는 현대 딥러닝 기술의 핵심이 되었습니다. 특히 은닉층은 신경망이 복잡한 패턴을 학습하고 강력한 성능을 발휘할 수 있는 중요한 역할을 합니다.

이어지는 글에서는 ANN의 구조적 특징을 바탕으로 학습 과정과 그 원리에 대해 더 깊이 알아보겠습니다.